Na matemática existe o estudo da trigonometria, área especializada em analisar as medidas dos ângulos e os segmentos das figuras. Assim, de acordo com esses estudos, distinguiu-se três variações denominadas de funções trigonométricas. Assim, temos o seno, o cosseno e a tangente.
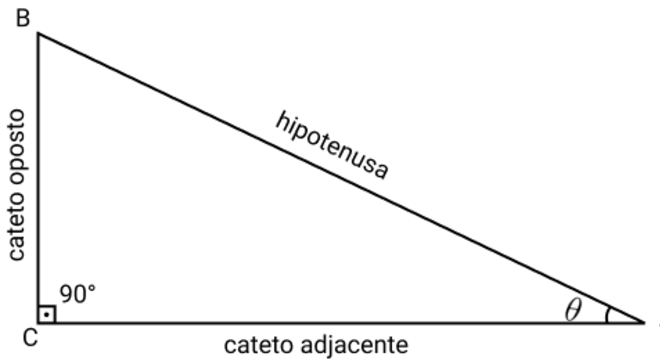
Dessa forma, os cálculos que envolvem distância e medidas de ângulos dependem, em grande parte, da trigonometria. Assim, uma das formas geométricas que utilizam desses conceitos é o triângulo retângulo.
Portanto, as funções trigonométricas estão relacionadas com os lados de um triângulo em decorrência do ângulo da figura. Ou seja, à essas relações damos o nome de seno, cosseno e tangente.
Definição de cosseno
Resumindo, o cosseno está relacionado à razão que existe entre a medida do cateto adjacente e a medida da hipotenusa. Ou seja, podemos representar essa afirmação com a seguinte fórmula:
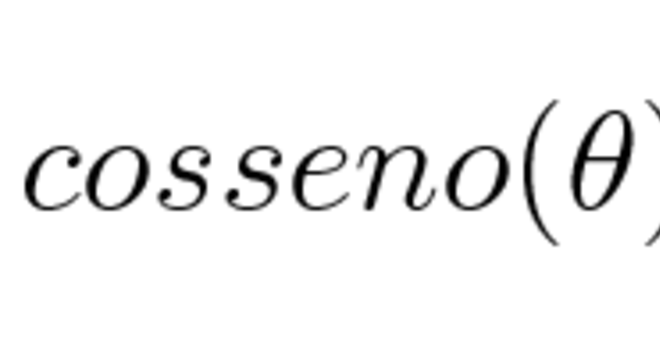
Ou seja, a fórmula é adquirida ao analisar a representação de um triângulo retângulo, figura geométrica que possui dois catetos e uma hipotenusa. Além disso, um triângulo retângulo é composto pelas retas que se encontram, chamadas de vértice, os lados- originados a partir do encontro das vértices, além dos ângulos internos e externos.
Área da circunferência – O que é, como calcular e exemplos na prática
×Valores trigonométricos do cosseno
Por se basear no figura do triângulo retângulo que possui ângulo de 90º, alguns valores trigonométricos foram definidos a partir disso. Ou seja, de acordo com a história, acredita-se que Hiparco de Niceia, por volta de 140 a.C, desenvolveu valores se baseando nos ângulos de 0ª a 90ª para as definições trigonométricas.
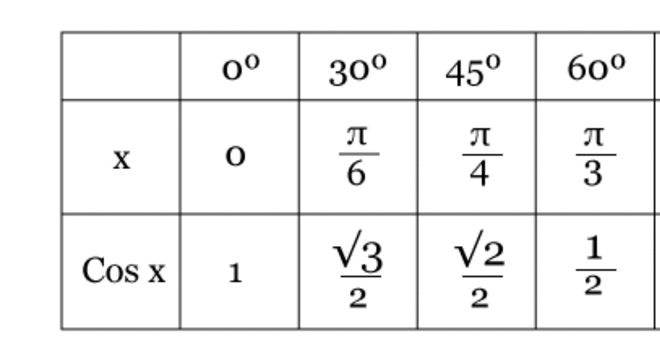
Assim, os valores do cosseno são:
30º – 3√ / 2 45° – 2√ / 2 90° – 1/2De acordo com o círculo trigonométrico em que existem quatro quadrantes, a função de cosseno segue algumas especificidades. Ou seja, de acordo com a função de cosseno, temos as seguintes definições:
O cosseno se encontra sob o eixo das abscissas (x); Assim, é é positivo no 1º e 4º quadrantes. Logo, no 2º e 3º quadrantes os valores assumem forma negativa; No primeiro e segundo quadrantes a função f é decrescente; 2º e 4º quadrantes a função f é crescente; Ângulos notáveisOs ângulos notáveis dizem respeitos à ângulos que não necessitam de fórmulas e cálculos muito rebuscados. Ou seja, é possível encontrar o valor de forma fácil quando esses estão relacionados aos ângulos 30°, 45° e 60°. Assim, observe na figura como os valores dos ângulos notáveis se dispõem:
A lei dos cossenos
Os cálculos utilizados no triângulo retângulo são, de certa forma, fácies. Isso porque, possuem os valores dispostos em relação às funções trigonométricas. Entretanto, existem casos em que os ângulos não estão presentes, devido o triângulo retângulo utilizar valores que vão de 0º a 90º.
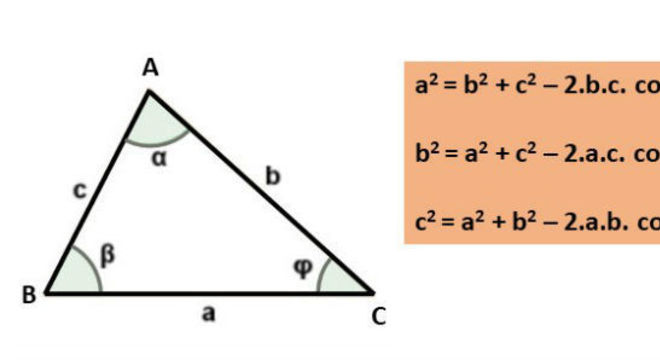
Nesse sentido, a lei dos cossenos é utilizada quando o triângulo não é retângulo. Ou seja, quando trata-se apenas de triângulo. Dessa forma, para que os cálculos sejam realizados é necessário utilizar a seguinte fórmula:
a² = b² + c² – 2ab CosA
b² = a + c² – 2ac CosB
c² = a + b² – 2ac CosC
Exemplo
Observe a figura à baixo:
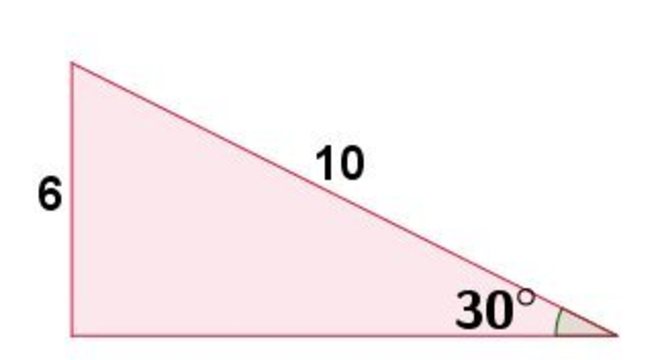
Na figura, é possível notar que existe um ângulo de 30º. Ou seja, o valor de cosseno que corresponde à esse ângulo é 3√ / 2. Então, qual o valor de x?
Assim, temos:
cos (30º) = x / 10
3√2 = x / 10
2x = 10 √3
x = 10√3 / 2
Resposta: x = 5√3
Você sabia?
A trigonometria é utilizada em diversas áreas além da matemática, como na economia, na cartografia e na biologia; As razões trigonométricas são os temas mais frequentes nos estudos da trigonometria;O que achou da matéria? Se gostou, corre e confere o que é Geometria Analítica e como resolver Operações com conjuntos.
Fontes: Educa mais Brasil e Info Escola
Fonte imagem destaque: Matemática Básica
Essa matéria Cosseno – Definição, valores trigonométricos, função e leis dos cossenos foi criada pelo site Conhecimento Científico.