Antes de tudo, você sabe a diferença entre figuras planas e figuras espaciais? A Geometria plana é a área da matemática que estuda as figuras planas. Ou seja, aquelas que possuem comprimento e largura, sendo figuras bidimensionais (duas dimensões). Sendo elas: círculo, quadrado, triângulo, retângulo, trapézio, hexágono, pentágono, paralelogramo e losango.
O que as difere das figuras geométricas espaciais é que estas apresentam três dimensões e incluem, portanto, o conceito de volume. Sendo elas: cilindro, cubo, dodecaedro, tetraedro, octaedro, icosaedro, cone, esfera, paralelepípedo e a pirâmide.
Sendo assim, na matéria de hoje, vamos conceituar o que são figuras planas, quais são, e como calcular o perímetro e a área desses polígonos.
O que é um Polígono?
Uma figura plana nada mais é que uma região plana fechada por segmentos de reta (no mínimo três segmentos).
Portanto, todas as figuras planas com três ou mais lados, são chamadas de Polígonos. Veja abaixo quais são:
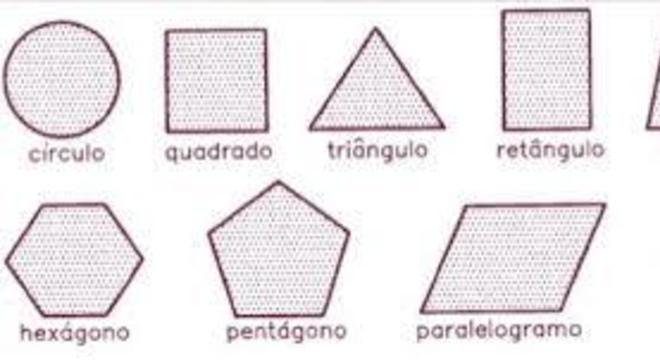
Fonte: Piraquara
Cada uma dessas formas geométricas possuem fórmulas matemáticas específicas para o cálculo da medida de seus perímetros e de suas superfícies (ou áreas). A seguir, vamos conhecer melhor cada uma.
Circunferência – O que é, características e geometria analítica
×Principais Figuras Planas
Antes de apresentar as fórmulas das áreas e como calcular o perímetro das figuras planas, devemos atentar para cada uma delas:
TrianguloÉ um polígono formado por três lados. São classificados de acordo com as medidas dos lados, bem como seus ângulos:
Quanto a medida dos lados:
Triângulo Equilátero: apresenta lados e ângulos internos iguais (60°); Triângulo Isósceles: apresenta dois lados e dois ângulos internos congruentes; Triângulo Escaleno: apresenta todos os lados e ângulos internos diferentes.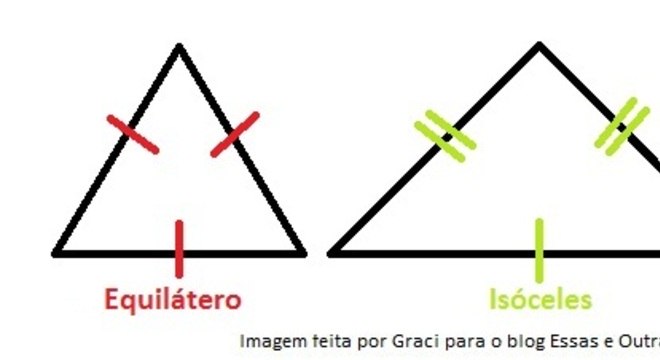
Quanto a medida dos ângulos:
Triângulo Retângulo: possui um ângulo interno de 90°; Triângulo Obtusângulo: possui dois ângulos agudos internos, ou seja, menor que 90°, e um ângulo obtuso interno, maior que 90°; Triângulo Acutângulo: possui três ângulos internos menores que 90°.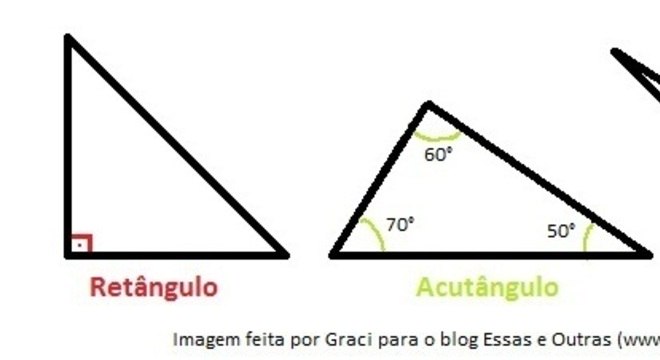
É um quadrilátero formado por quatro lados, dois deles na vertical e dois na horizontal. Da mesma forma que o quadrado, ele apresenta quatro ângulos internos de 90° (retos).
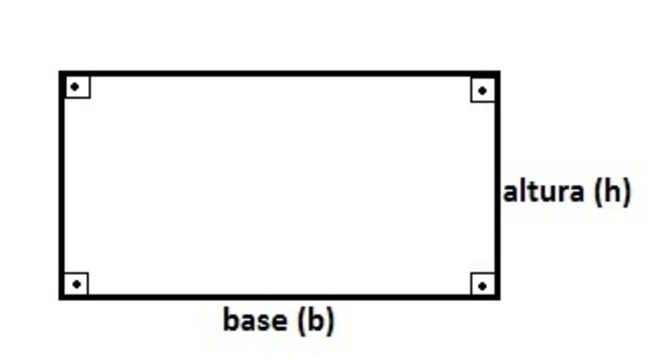
É um quadrilátero regular formado por quatro lados congruentes (mesma medida). Ele é formado por quatro ângulos internos de 90°, os quais são chamados de ângulos retos.
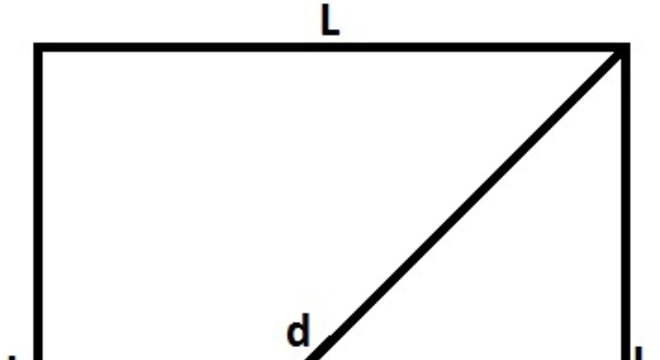
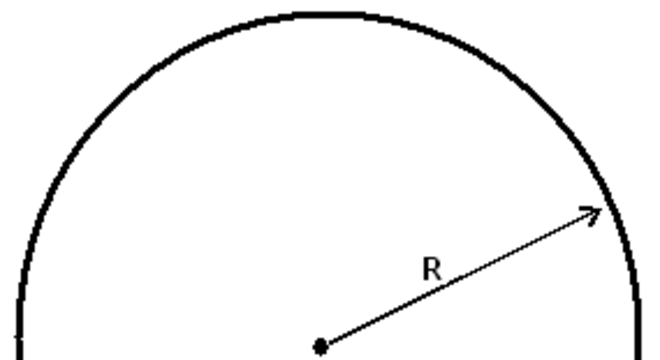
Figura plana também chamada de disco. Apresenta uma forma circular. O raio do círculo representa a medida entre o ponto central da figura e uma das extremidades.
Já o diâmetro equivale duas vezes o raio, posto que representa o segmento de reta que passa pelo centro do círculo, dividindo-o em duas metades iguais.
É um quadrilátero notável com dois lados e bases paralelas, donde uma é maior e outra menor. A soma de seus ângulos internos totaliza 360°. São classificados em:
Trapézio Retângulo: apresenta dois ângulos de 90º (ângulos retos); Trapézio Isósceles: também chamado de trapézio simétrico donde os lados não paralelos possuem a mesma medida; Trapézio Escaleno: todos os lados apresentam medidas diferentes.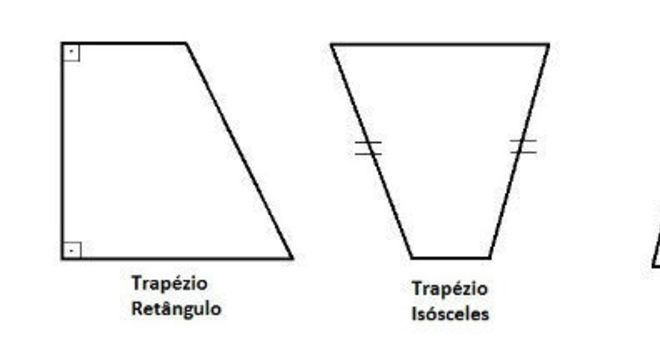
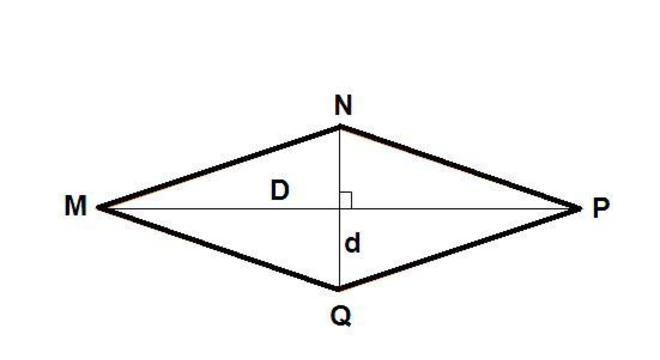
É um quadrilátero equilátero formado por quatro lados iguais. Apresenta dois lados e ângulos opostos congruentes e paralelos, com duas diagonais que se cruzam perpendicularmente. Além disso, ele possui dois ângulos agudos (menores que 90º) e dois ângulos obtusos (maiores que 90º).
Sendo assim, a seguir vamos aprender como calcular o perímetro e as suas superfícies de cada figura plana.
Cálculo do Perímetro em Figuras Planas
O perímetro de uma figura plana é simplesmente a soma das medidas de todos os lados dessa figura. Por exemplo, quando você dá a volta em um quarteirão, você percorreu a distância do Perímetro do quarteirão.
Para melhor entendimento, observe a figura abaixo. Ela representa uma figura plana de quatro lados (portanto é um quadrilátero), denominada trapézio.
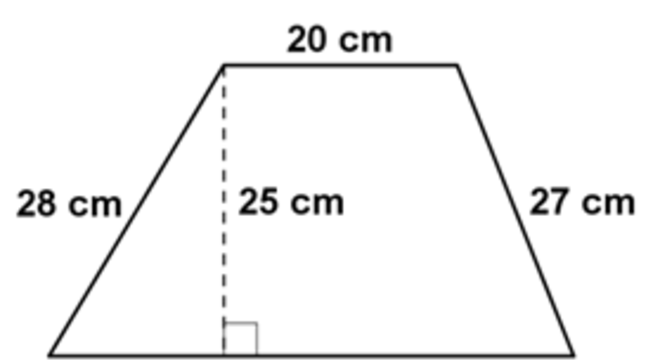
Então como você pode ver, as medidas de seus lados valem 42,7 cm, 27 cm, 20 cm e 28 cm. Como todas as medidas dos lados da figura são conhecidas, podemos calcular o perímetro através da soma dos lados:
Portanto, fica assim: soma dos lados = 42,7 + 27 + 20 + 28 = 117,7 cm.
Obs.: O perímetro é uma grandeza cuja unidade de medida é a de comprimento e, portanto, pode ser medido em metros ou em seus múltiplos e submúltiplos.
Cálculo da Área em Figuras Planas
Conforme visto anteriormente, é possível calcular a área das figuras planas. Mas afinal, o que é área e como ela é calculada?
Área é a denominação dada à medida de uma superfície. Desse modo, podemos pensar que quanto maior a superfície da figura, maior será sua área.
Obs.: O valor da área será dado sempre em cm2, m2 ou km2.
Portanto, cada uma das figuras planas possuem fórmulas específicas para o cálculo de sua área. Vejamos então:
TriânguloPara encontrar a área de um triângulo retângulo (que possui um ângulo de 90º), dividimos por 2 o resultado da multiplicação da base (b) pela altura (h), que é calculada a partir da distância do vértice à base. Assim, chegamos à fórmula:
A = b.h/2No caso dos triângulos equiláteros (que possuem todos os lados iguais e ângulos internos de 60º), a fórmula padrão utilizada então é:
A = L2 √3/4No entanto, quando falamos de triângulos que não possuem o ângulo de 90º, utilizamos fórmulas que exigem o conhecimento de conceitos como seno e cosseno, semiperímetro ou que são formadas a partir do raio de uma circunferência traçada em volta ou dentro do triângulo.
RetânguloA fórmula utilizada para determinar a área de um retângulo é uma das mais simples da geometria. Basta multiplicar a base pela altura. Sendo assim, chegamos na seguinte forma:
A = b.h QuadradoA fórmula para o cálculo de área de um quadrado segue a mesma lógica do retângulo. No entanto, considerando que esta figura possui os 4 lados iguais, basta descobrir a medida de um dos lados e elevar este número ao quadrado. Assim, chegamos à fórmula:
A = L2 CírculoNa figura do círculo, em que temos a constante π e o raio, representado pela letra R, basta elevar este último ao quadrado e, na sequência, multiplicar os valores, de acordo com a seguinte fórmula:
A = πR2Obs.: circunferência é o nome dado à linha de contorno do círculo. Portanto, por ser uma linha, calcula-se o seu perímetro usando a expressão: C = 2.π.r
TrapézioNo caso de trapézio, precisamos multiplicar a altura (h) pelo valor da soma da base maior e da base menor, representadas respectivamente por B e b, e, na sequência, dividir o valor por 2. Sendo assim, chega na seguinte fórmula:
A = (B + b) . h/2 LosangoPara descobrir a área total do losango, basta multiplicar o valor da diagonal maior (D) e da menor (d) e em seguida, dividir o resultado por 2, de acordo com a fórmula:
A = D.d/2.
Então, gostou dessa matéria sobre figuras planas?
Portanto, agora que você sabe quais são e como calcular o perímetro e suas áreas, fique por dentro também da Trigonometria.
Fontes: Blog do Enem, Toda Matéria
Fonte Imagem Destaque: Canal Smile and Learn
Essa matéria Figuras Planas – O que são, quais são, como calcular perímetro e área foi criada pelo site Conhecimento Científico.