Na Matemática existem diversas fórmulas e equações que simplificam a resolução de operações matemáticas, como no caso dos logaritmos. Basicamente, o logaritmo representa o número da base que precisa ser igual ao expoente de determinada potência.
Sendo assim, o que os logaritmos fazem é transformar os produtos em soma, bem como subtrações e potências em multiplicações. Para isso, é necessário elevar a base, de maneira que a potência ax, por exemplo, se iguale a b. Neste caso, a e b precisam ser números reais e positivos, além de a≠1.
Em síntese, os logaritmos surgiram para que contas matemáticas possam ser resolvidas de forma mais simples. O primeiro a utilizar o termo foi o matemático John Napier, onde conseguiu representar os resultados das contas em operações matemáticas.
Porém, antes de entender o que os logaritmos representam, é necessário compreender sobre as propriedades da potenciação. Então, vamos lá!
Definição de logaritmo
Um logaritmo é uma equação matemática na qual existe uma base e um número que precisa ser elevado para que o expoente da operação seja encontrado. Dessa forma, temos que: logaritmo de a na base b, representado por logab.
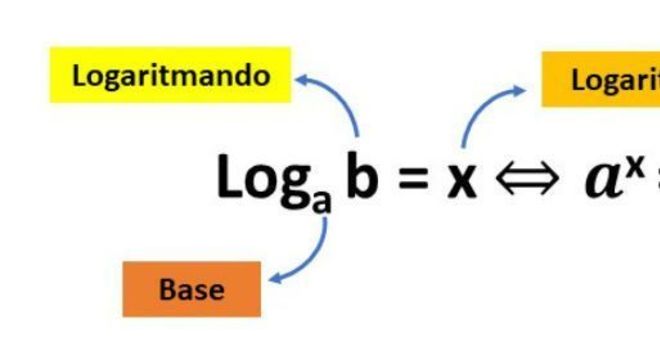
Neste caso, o valor de x representa o o número que devemos elevar para que o o expoente seja revelado. Vamos analisar o exemplo de log28, onde lê-se logaritmo de 8 na base 2. Aqui, o que devemos procurar é o número que, elevado a 2 dê o resultado de 8.
Portanto, temos: Log28 = 3, pois 2³ = 8.
Na equação, o x representa o logaritmo, b é a base e a é o logaritmando. Nesse sentido, vale lembrar que, quando o valor da base não é fornecido, significa que b será igual a 10, ou seja, Log a.
Para melhor compreender o conceito de logaritmo, observe os exemplos a seguir:
a) log381 = 4, pois 34 = 81. b) log100 = 2, pois 10² = 100 (como não havia valor para a base, ela é igual a 10). c) log21024 = 10, pois 210 = 1024.Propriedades
Assim como outras equações matemáticas, os logaritmos possuem propriedades que devem ser analisadas, como ocorrem com as propriedades das potências. A primeira delas é que, quando o valor de uma equação for igual a 1, então a base será sempre 0, já que todo número elevado a 0 é igual a 1.
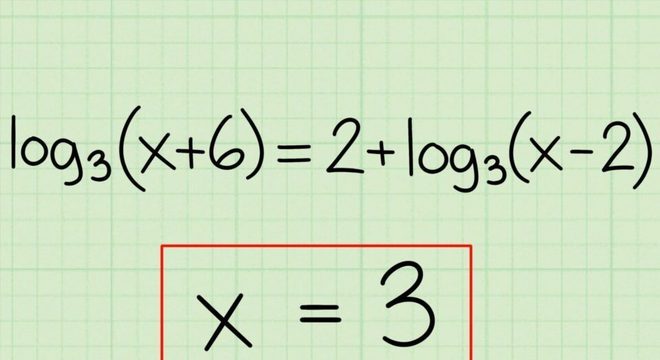
Por exemplo: log81 = 0, pois 80 = 1.
Outra propriedade é referente à base elevada a 1. Ou seja, quando determinada base for elevada 1 o resultado será sempre ele mesmo. Então, temos que o log de base e o logaritmando serão sempre iguais ao próprio número da base. Observe o exemplo: log55 = 1, pois 5¹ = 5.
Agora, caso dois logaritmos de uma mesma base são iguais, o logaritmando também será igual. Por exemplo: logb8 = logba, então a = 8.
Sendo assim, temos quatro propriedades que definem a forma como estas equações matemáticas devem ser resolvidas, sendo elas:
Logaritmo de um produto: o produto da equação será sempre igual a soma de todos os seus logaritmos: Loga (b.c) = Loga b + loga c; Logaritmo de um quociente: representa o quociente onde o valor é igual a diferença do resultado da equação; Potência: é o valor igual ao produto da potência pelo logaritmo: Loga bm = m . Loga b; Mudança de base: a base de um logaritmo pode ser mudada utilizando a seguinte equação: log bc = log ac / log ab.Então, o que achou da matéria? Já que está aqui, aproveita pra conferir o que é a Teoria dos Conjuntos e o que são Conjuntos Numéricos.
Fontes: Mundo Educação, Toda Matéria, Brasil Escola e Info Escola
Imagens: Instituto Claro, Toda Matéria e WikiHow
Essa matéria Logaritmos, o que são? Definição, propriedades e como calcular foi criada pelo site Conhecimento Científico.